You are currently studying
Grade 9 → Math → Number Systems → 1.1-Introduction
- Understand different types of number sets.
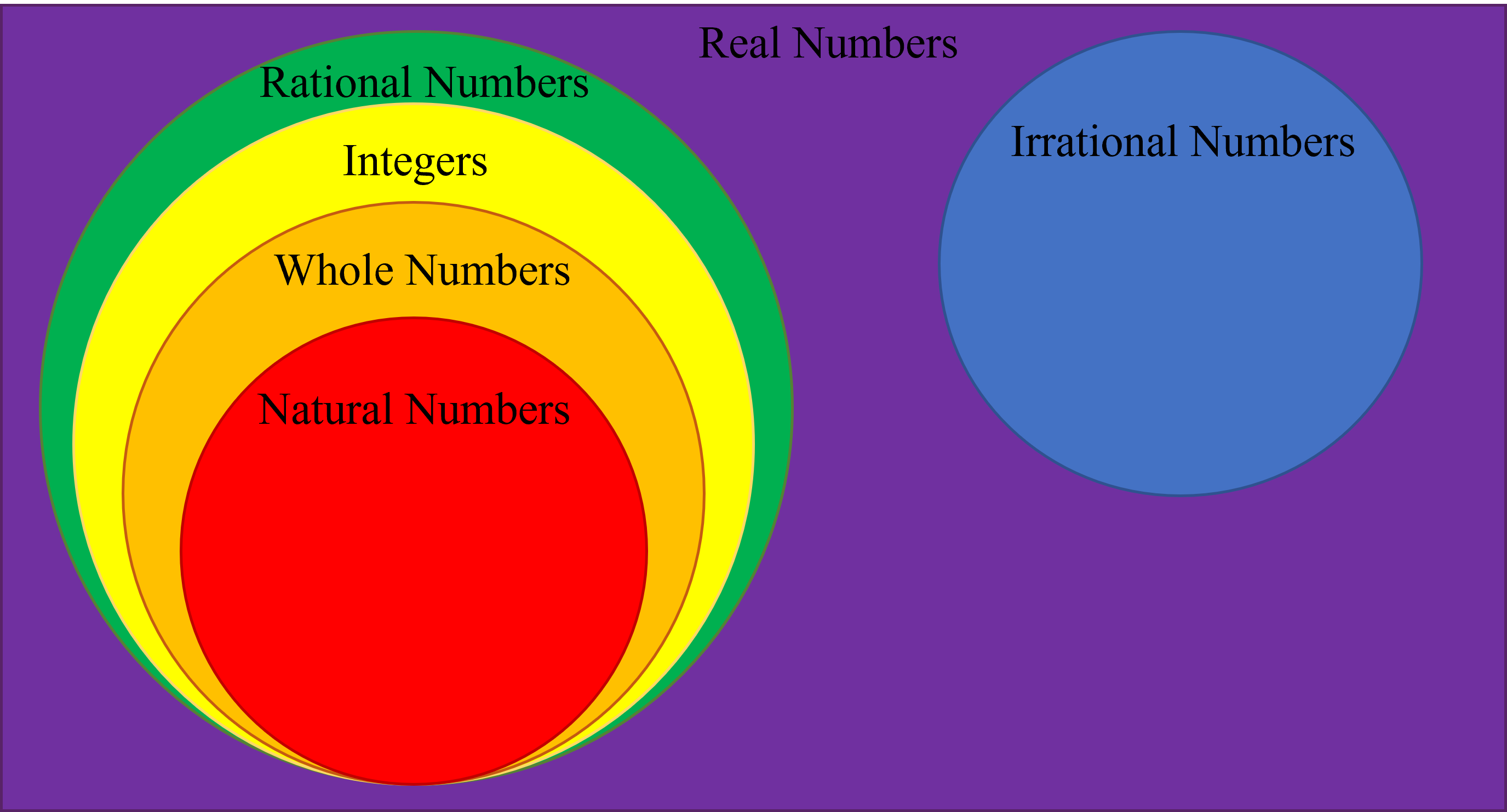
The different number sets are as follows:
- Natural Numbers: N = {1,2,3,4,.....}
- Whole Numbers: W = {0,1,2,3,4,.....}
- Integers: I= {....,-3,-2,-1-,0,1,2,3,4,.....}
- Rational Numbers: Integers + Fractions
- Irrational Numbers: numbers that cannot be represented as $\dfrac{p}{q}$
Solved Example: 1-1-01
Is zero a rational number? Can you write it in the form $\dfrac{p}{q}$ where p and q are integers and q $\neq$ 0?
Check Answer
Solution:
Is Zero a Rational Number?
Yes, zero is a rational number. It can be expressed in the form $\dfrac{p}{q}$ where $p = 0$ and $q = 1$. Here, both 0 and 1 are integers, and since $q \neq 0$, this satisfies the definition of a rational number.
Solved Example: 1-1-02
Find six rational numbers between 3 and 4.
Check Answer
Solution:
Six Rational Numbers Between 3 and 4
To find six rational numbers between 3 and 4, consider fractions. The following are examples:
$\dfrac{22}{7}$
$\dfrac{23}{7}$
$\dfrac{24}{7}$
$\dfrac{25}{7}$
$\dfrac{26}{7}$
$\dfrac{27}{7}$
These values are all between 3 and 4.
Solved Example: 1-1-03
Find five rational numbers between $\dfrac{3}{5}$ and $\dfrac{4}{5}$.
Check Answer
Solution:
Five Rational Numbers Between $\dfrac{3}{5}$ and $\dfrac{4}{5}$
To find five rational numbers between $\dfrac{3}{5}$ and $\dfrac{4}{5}$, consider the following:
$\dfrac{31}{50}$
$\dfrac{32}{50}$
$\dfrac{33}{50}$
$\dfrac{34}{50}$
$\dfrac{35}{50}$
These fractions are all greater than $\dfrac{3}{5}$ and less than $\dfrac{4}{5}$.
Solved Example: 1-1-04
State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
Check Answer
Solution:
True or False Statements
(i) True: Every natural number (1, 2, 3, ...) is included in the whole numbers (0, 1, 2, ...).
(ii) False: Whole numbers include 0, while integers include negative numbers, so not every integer is a whole number.
(iii) False: Rational numbers can be fractions, such as $\dfrac{1}{2}$, which are not whole numbers.