A polynomial in one variable is an expression that consists of terms, each of which is a product of a constant (called the coefficient) and a variable raised to a non-negative integer exponent. The general form of a polynomial in one variable $x$ can be expressed as:

$P(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0$

where:

• $a_n, a_{n-1}, \ldots, a_1, a_0$ are constants (coefficients).
• $n$ is a non-negative integer, indicating the degree of the polynomial.
• The term $a_n x^n$ is the leading term, and $a_n$ is the leading coefficient.

The degree of a polynomial is the highest power of the variable in the polynomial. For example, in the polynomial:

$P(x) = 4x^3 + 3x^2 - 2x + 7$

the degree is 3, and the leading coefficient is 4.

Types of Polynomials

Polynomials can be classified based on their degree:

• Constant Polynomial: Degree 0. Example: $P(x) = 5$.
• Linear Polynomial: Degree 1. Example: $P(x) = 3x + 2$.
• Quadratic Polynomial: Degree 2. Example: $P(x) = x^2 - 4x + 4$.
• Cubic Polynomial: Degree 3. Example: $P(x) = 2x^3 + 3x^2 - x + 1$.
• Quartic Polynomial: Degree 4. Example: $P(x) = x^4 - 2x^3 + 3$.
• Quintic Polynomial: Degree 5. Example: $P(x) = 5x^5 + x$.

Standard Form of a Polynomial

The standard form of a polynomial is when it is expressed in descending order of the degree of the terms. For example, the polynomial:

$P(x) = 2 + 3x^2 - x + 4x^3$

can be rearranged in standard form as:

$P(x) = 4x^3 + 3x^2 - x + 2$.

Operations on Polynomials

Polynomials can be added, subtracted, and multiplied as follows:

• Addition: To add two polynomials, combine like terms. Example:

If $P(x) = 2x^2 + 3x + 1$ and $Q(x) = x^2 - 2x + 4$, then:

$P(x) + Q(x) = (2x^2 + x^2) + (3x - 2x) + (1 + 4) = 3x^2 + x + 5$.

• Subtraction: To subtract polynomials, subtract like terms. Example:

If $P(x) = 3x^2 + 4x$ and $Q(x) = 2x^2 + x$, then:

$P(x) - Q(x) = (3x^2 - 2x^2) + (4x - x) = x^2 + 3x$.

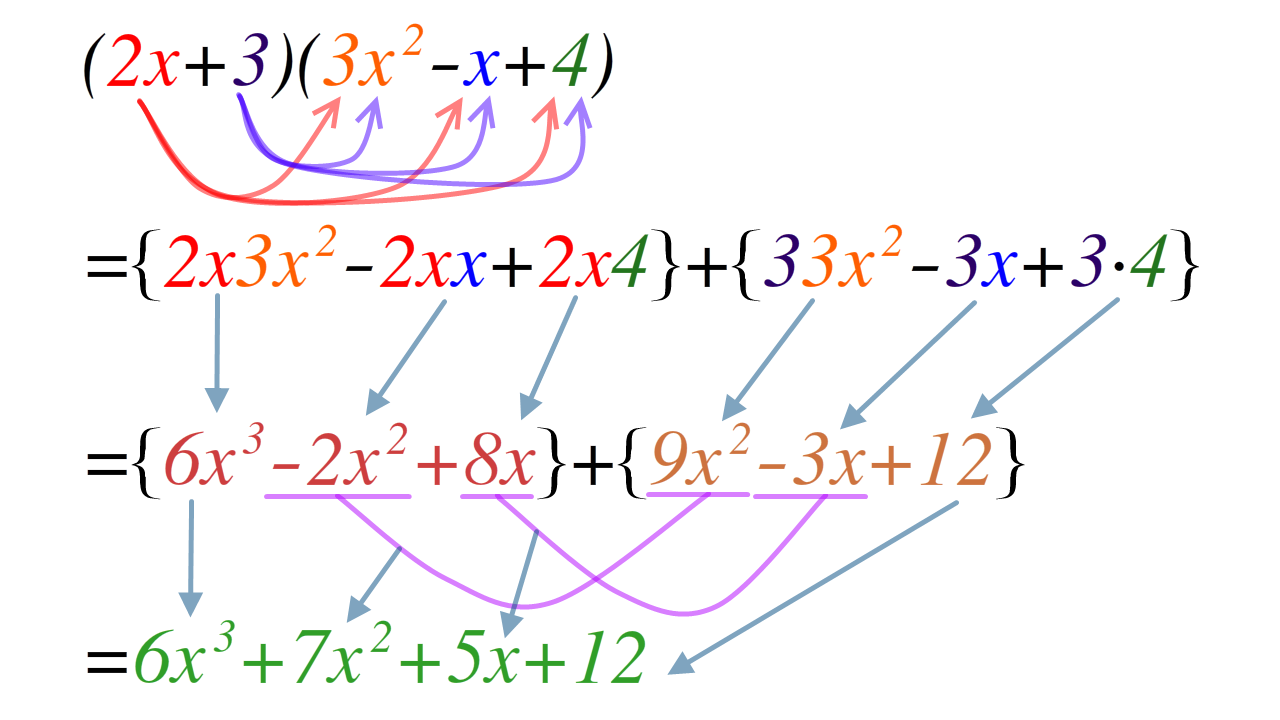
• Multiplication: Multiply each term in the first polynomial by each term in the second polynomial. Example:

If $P(x) = x + 1$ and $Q(x) = x - 2$, then:

$P(x) \cdot Q(x) = (x)(x) + (x)(-2) + (1)(x) + (1)(-2) = x^2 - 2x + x - 2 = x^2 - x - 2$.