7.3-More Criteria for Congruence of Triangles

7.3-More Criteria for Congruence of Triangles Important Formulae

You are currently studying
Grade 9 → Math → Triangles → 7.3-More Criteria for Congruence of Triangles

After successful completion of this topic, you should be able to:

  • Understand various criterions for congruence of triangles.

(SSS congruence rule) : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.:
(RHS congruence rule) : If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.:


Somebody762, CC BY-SA 3.0, via Wikimedia Commons


Somebody762, CC BY-SA 3.0, via Wikimedia Commons


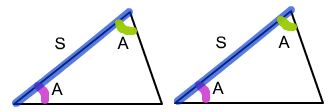
Somebody762, CC BY-SA 3.0, via Wikimedia Commons


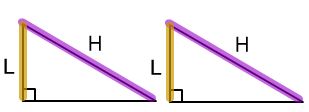
Somebody762, CC BY-SA 3.0, via Wikimedia Commons

∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that:

(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.

AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:

(i) AD bisects BC
(ii) AD bisects ∠ A.

Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆ PQR (see Fig. 7.40). Show that:

(i) ∆ ABM ≅ ∆ PQN
(ii) ∆ ABC ≅ ∆ PQR

Solution:
(ii) From (i) ,∠ABM =∠PQN

Suggest improvements/Report errors

BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠ B = ∠ C.